[2514] 計算方法を教えて下さい
投稿者:こて
投稿日:2008年09月28日 (日) 19時23分

|
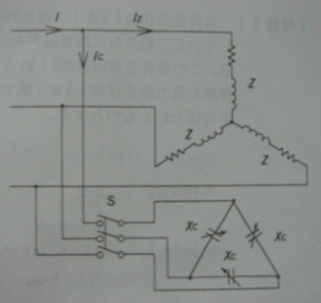 |
線間電圧が200[V]で周波数が50[Hz]の平衡三相配電線に、一相のインピーダンスがZ[Ω]の三相平衡負荷と一相のリアクタンスがXc[Ω]の可変コンデンサが並列に接続されています。スイッチSが開いているとき、20[Kw]の有効電力が消費され、その力率は0.8(遅れ)であった。Xc=5[Ω]として、Sを閉じたときのつぎの値を教えて下さい。
(1)負荷回路全体の有効電力P[Kw]
(2)負荷回路全体の無効電力Q[Kvar]
(3)負荷回路全体の皮相電力S[KVA]
(4)インピーダンスZに流れる電流Iz[A]
(5)コンデンサに流れる電流Ic[A]
(6)線路電流I[A]
(7)線路電流を最小にするためのコンデンサのリアクタンス値Xc
(8)前項(7)のコンデンサの静電容量値
以上の計算式を教えて下さい。 |
■[2515] 2514電験初受験(2008年09月29日 (月) 23時14分)
 |
19年度理論問15が類似しているかな? |
|
■[2516] 計算 鹿の骨(2008年10月02日 (木) 23時09分)
 |
(1)負荷回路全体の有効電力P[Kw]
コンデンサは有効電力を消費しないのでコンデンサの並列解列の如何は有効電力の値に関係有りません。
従って並列前の有効電力=20[kW]のままです。
(2)負荷回路全体の無効電力Q[Kvar]
コンデンサ1基が消費する無効電力Qcは下記になります。
Qc=200[V]∠±0×200[V]∠±0÷5[Ω]∠-90
=8000[var]∠90=8[kvar]∠90=j8[kvar]
3基のコンデンサの消費する無効電力の和はこの3倍ですから
ΣQ[var]=8[kvar]∠90×3=24[kvar]∠90=j24[kvar]
元々の回路の消費有効電力が20[kW]で力率が0.8遅れですから、コンデンサを並列する前の回路の無効電力ΣQLは
ΣQL=20÷0.8×0.6=15[kvar]∠-90=-j15[kvar]
コンデサ並列後の回路全体の無効電力Qは
Q=ΣQc+ΣQL=j24[kvar]-j15[kvar]=j9[kvar]となります。
(3)負荷回路全体の皮相電力S[KVA]
S=√(P^2+Q^2)ですから
=√(20^2+9^2)=√481=21.93[kVA]となります。
(4)インピーダンスZに流れる電流Iz[A]
コンデンサを並列する前の回路の皮相電力ΣSは
ΣS=20÷0.8=25[kVA]
電流Izと皮相電力ΣSと線間電圧との関係式は下記です。
皮相電力ΣS=√3×線間電圧×電流Iz
電流Iz=皮相電力ΣS÷√3÷線間電圧×1000=25[kVA]÷√3÷200[V]×1000=72.2[A]となります。
(5)コンデンサに流れる電流Ic[A]
コンデンサ1基分を計算すればOKです。
コンデンサ電流Ic=200[V]÷5[Ω]=40[A]となります。
(6)線路電流I[A]
負荷回路全体の皮相電力S[KVA]=21.93[kVA]ですから線電流Iは
I=S[kVA]÷200[V]÷√3×1000=21.93[kVA]÷200[V]÷√3×1000=63.3[A]となります。
(7)線路電流を最小にするためのコンデンサのリアクタンス値Xc[Ω]
コンデンサの容量は24[kvar]になっていますが、インピーダンスZの無効電力は15[kvar]です。
コンデンサの容量が15[kvar]になれば丁度力率=100[%]になります。
コンデンサのリアクタンス値が5[Ω]の時に24[kvar]でしたから求めるXc[Ω]は下記の式になります。
1/5:1/Xc=24:15
24/Xc=15/5
Xc=8[Ω]となります。
(8)前項(7)のコンデンサの静電容量値
コンデンサの静電容量値C[F]、周波数f[Hz]とリアクタンスXc[Ω]との関係式は
Xc=1/(2πfC)
C=1÷8÷(2×3.1415×50)×1、000、000=398[μF]となります。
これで合っていますか?
|
|
■[2517] こて(2008年10月04日 (土) 00時31分)

 |
鹿の骨さん、大変わかりやすくありがとうございました。 |
|
■[2518] こて(2008年10月04日 (土) 01時03分)

 |
鹿の骨さん、すいませんが、最後の(8)の1÷8÷(2×3.1415×50)×1000000の8はどこからでてきたのでしょうか? |
|
■[2519] 鹿の骨(2008年10月04日 (土) 13時46分)
 |
Xc=1/(2πfC)の式に値を代入すれば自動的にこの式になります。
Xc=8[Ω]
π=3.1415・・・
f=50[Hz]
1000000は[μ]の換算係数です。
Xc=1/(2πfC)が関係式ですからこの式に値を代入すると下記になります。
8[Ω]=1/(2×3.1415×50[Hz]×C[F])
C[F]=1÷8[Ω]÷(2×3.1415×50[Hz])×1、000、000=398[μF] |
|
■[2523] こて(2008年10月05日 (日) 20時42分)

 |
大変ありがとうございました。 |
|
■[2604] 気になったことがありますぽち(2009年05月28日 (木) 10時58分)
 |
はじめまして。
いつも勉強させていただいております。
鹿の骨様の解答で一つ気になった事がありますので投稿させてもらいました。
(5)コンデンサに流れる電流Ic[A]
コンデンサ1基分を計算すればOKです。
コンデンサ電流Ic=200[V]÷5[Ω]=40[A]となります。
図を見るとIcは線電流に見えるのですが、この解答だとコンデンサ一基分の相電流に思えるのですが。。。
Ic=40[A]×√3
ではと考え込んでしまいました。 |
|
| |